CONTACT US

Bachelor of Science in Mathematics


The BS Mathematics Program is one of the undergraduate programs that UP Baguio (then UP College Baguio) has offered since 1975. Evolving from the BS Physics-Mathematics program, the first batch graduated in 1977. The original BS Mathematics program provided training for teaching, research, or jobs related to statistics, operations research, business management, and more. The current BS Mathematics program is a four-year program that provides solid undergraduate preparation in mathematics. The curriculum covers fundamental and abstract concepts in mathematics and important and emerging fields in applied mathematics. The program allows the students to study different fields in Mathematics, such as Algebra (linear, abstract), Analysis (elementary, advanced, real, complex, numerical), and other areas like Statistics (elementary, mathematical, applied), Modern Geometry, Number Theory, Combinatorics, and Topology.

PROGRAM OBJECTIVES

The program's objectives focus on achieving a balance between pure mathematics and some of its areas of application. It aims to develop the student's understanding of the content and the methodology of basic mathematical disciplines to prepare him/her for advanced studies, research, for careers in industry and government and for teaching undergraduate mathematics courses.

PROGRAM LEARNING OUTCOMES

 PLOs   Generic Program Learning Outcomes 
PLO 1 Promote engagement in lifelong learning towards excellence in the field of expertise.
PLO 2 Apply professional, social, and ethical responsibilities as active and participative citizens.
PLO 3 Develop social and professional skills to build healthy, productive, and ethical working relationships with peers.
 Specific Program Learning Outcomes 
PLO 4 Develop mastery in the core and applied areas of mathematics.
PLO 5 Develop skills in pattern recognition, abstraction, critical analysis, and problem- solving, and in making generalizations, synthesis, and rigorous arguments.
PLO 6 Develop an enhanced perception of the strength and importance of mathematics in the modern world including inter-relationships within mathematics and its connections to the natural sciences, humanities and the arts, and the social sciences.
PLO 7 Analyze current advances in mathematics research and propose conjectures that extend the theory.


I. CORE COURSES (16 UNITS)

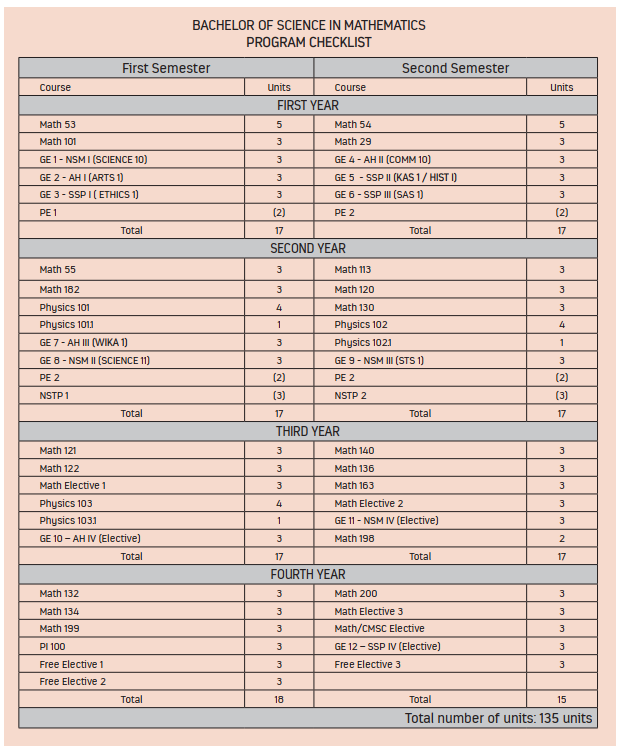
CourseCourse TitlePrereq.Units
Math 29Basic Concepts in MathematicsNone3.0
Math 53Elementary Analysis INone5.0
Math 54Elementary Analysis IIMath 535.0
Math 55Elementary Analysis IIIMath 543.0

II. MAJOR COURSES (44 UNITS)

CourseCourse TitlePrereq.Units
Math 101Elementary StatisticsNone3.0
Math 113Differential EquationsMath 553.0
Math 120Algebraic Structures IMath 293.0
Math 121Algebraic Structures IIMath 1203.0
Math 122Linear Algebra and Matrix TheoryMath 293.0
Math 130Mathematical AnalysisMath 553.0
Math 132Real AnalysisMath 553.0
Math 134Complex AnalysisMath 553.0
Math 136Introduction to Numerical AnalysisMath 113, 1223.0
Math 140Topological StructuresJS3.0
Math 163Mathematical StatisticsMath 553.0
Math 182Introduction to Computer ProgrammingMath 543.0
Math 198SeminarCOI3.0
Math 199Research in MathematicsCOI3.0
Math 200Undergraduate ThesisMath 1993.0

III. QUALIFIED ELECTIVES (12 UNITS)

CourseCourse TitlePrereq.Units
Math 123Elementary Theory of NumbersMath 29 or CMSC 553.0
Math 133Introduction to Functional AnalysisMath 1303.0
Math 150Modern GeometryMath 553.0
Math 160Probability TheoryCOI3.0
Math 170Foundations of MathematicsMath 29 or CMSC 553.0
Math 181Mathematical Methods of Operation ResearchMath 122 or CMSC 1163.0
Math 190Issues in Mathematics EducationMath 543.0
CMSC 161Interactive Computer GraphicsCMSC 116 or Equivalent3.0
CMSC 162Artificial IntelligenceCMSC 1233.0
CMSC 198PracticumCOI3.0

IV. PHYSICAL SCIENCES COURSES (15 UNITS)

CourseCourse TitlePrereq.Units
Physics 101Fundamental Physics I (lec)Coreq: Math 534.0
Physics 101.1Fundamental Physics I (lab)Coreq: Physics 1011.0
Physics 102Fundamental Physics II (lec)Physics 101, Physics 101.1, and Math 534.0
Physics 102.1Fundamental Physics II (lab)Coreq: Physics 1021.0
Physics 103Fundamental Physics III (lec)Physics 102, Physics 102.1, and Math 544.0
Physics 103.1Fundamental Physics III (lab)Coreq: Physics 103.11.0

V. GE Requirements (36 UNITS)

A. Natural Sciences and Math (NSM) - 12 UNITS
CORE Science 10, Science 11, STS 1
ElectiveMath 10, Chem 1, Geol 1
B. Arts and Humanities (AH) - 12 UNITS
CoreArts 1, Comm 10, Wika 1
ElectivePhilarts 1, MS 11
C. Social Sciences and Philosophy (SSP) - 12 UNITS
CoreEthics 1, History 1, Kasaysayan 1, SAS 1
ElectiveHist 3, Philo 27, Soc Sci 30

VI. Other Required Courses (12 UNITS)

CourseCourse Title
PI 100Life of Rizal
3 Free ElectivesAny electives from the 3 colleges
NSTPNSTP 1, NSTP 2
PEPE 1 (Required), any three from PE 2, PE 3 and PE 4

PROGRAM CHECKLIST

GE Requirements

A. Natural Sciences and Math (NSM) - 12 UNITS
CORE Science 10, Science 11, STS 1
ElectiveMath 10, Chem 1, Geol 1
B. Arts and Humanities (AH) - 12 UNITS
CoreArts 1, Comm 12, Wika 1
ElectivePhilarts 1, MS 11
C. Social Sciences and Philosophy (SSP) - 12 UNITS
CoreEthics 1, History 1, Kasaysayan 1, SAS 1
ElectiveHist 3, Philo 27, Soc Sci 30

CURRICULUM FLOWCHART



Download Flowchart

ACADEMIC POLICIES

  1. Retention Policy
    1. A B.S. Mathematics Student must pass the required minimum number of Math courses per semester according to the following table:
      2. No. of Math Courses Enrolled inMinimum No. of Courses to Pass
      11
      22
      32
      43
      53
      6 or more4
    2. A student who fails to satisfy provision no.1 for two consecutive terms (including midyear) shall be disqualified from the program.
    3. A student must pass the following Mathematics courses (Math 29, 53, 54, 55, and 101) in at most two takes; otherwise, he/she shall be disqualified from the program.
    4. If, after six semesters of enrollment of core courses, the student fails to complete all such Mathematics subjects, the student is automatically disqualified from the program.
  2. Readmission Policies
    1. The student must submit a letter of readmission addressed to the DMCS Chair.
    2. Considerations for readmission include the following: the number of units credited, the number of units and semesters remaining including application of the maximum residency rule, and the merit/strength of the reason for readmission. The adviser shall evaluate the merits of a student’s appeal for readmission and makes initial recommendation to the Department faculty who shall discuss and make final action on the appeal.
    3. If a student is readmitted, he/she shall be placed under probation and must satisfy the program’s retention policies. At the end of the semester, the student must get no grades of 4s, 5s, DRP, and INC in all Mathematics courses that he/she enrolled in. Failure to satisfy this provision would mean disqualification from the program.
  3. Shifting Policies
    • University rules on shifting shall apply.
    • Furthermore, to be admitted to the program: A student must have taken Math 53/equivalent with a grade of at least 2.5. If, in addition, the student has taken other Math courses, (except Math 1), he/she should have an average of at least 2.75.
  4. Waiver of prerequisite/co-requisite
    • No waiving of prerequisites is granted approval.

INSTRUCTIONAL POLICIES AND REQUIREMENTS

  1. Exams are departmental for multi-sections.
  2. All syllabi contain the following ground rules:
    1. Students are expected to have a copy of the textbook. Lectures and exercises will be based on the textbook.
    2. The University rules on class attendance (Article 346 of the University Code) shall be strictly enforced in this course.
    3. If a student misses a short quiz, his/ her grade in that quiz is zero. If a student misses a long exam for a valid reason (this requires documentation), his/ her grade in the final exam will account as his/ her grade for the missed exam. This applies to not more than one long exam missed. A student who fails to take any examination for invalid reasons will get a grade of 0% for that exam.
  3. Cheating, in any form, will not be tolerated.
    4. This quotation must be written on every long exam questionnaire:
    “Cheating is a form of intellectual dishonesty that will not be condoned. Anyone caught cheating shall be dealt with in accordance with the rules on student conduct and discipline. Cheating is punishable with a grade of “5.0” in the course and/or (1) suspension for a period of not less than one year; or (2) expulsion from the University.”
  4. Faculty members of multi-section courses should have a course leader and a regular discussion should be made concerning topics to be discussed and long exam preparations.
  5. If a take home exam is to be given, faculty must encourage students to have group discussions. Exams must purely be a problem solving type. If it is a group exam each group must be composed of at most 3 members and every member must submit his/her evaluation of other members.
  6. Other Policies:
    1. Blackboards should be erased after every class.
    2. Sharing of lecture transparencies is encouraged.
    3. Permission for make-up classes should be sought. There is no regular make up class.